VLSI DSP之展开

本节主要介绍了VLSI DSP中展开这一方法的基本概念与性质。

展开的基本概念

• 展开：是一种转换技术，它产生一个新的程序来描述原有程序的多次迭代，J称为展开因子，表示迭代次数

  

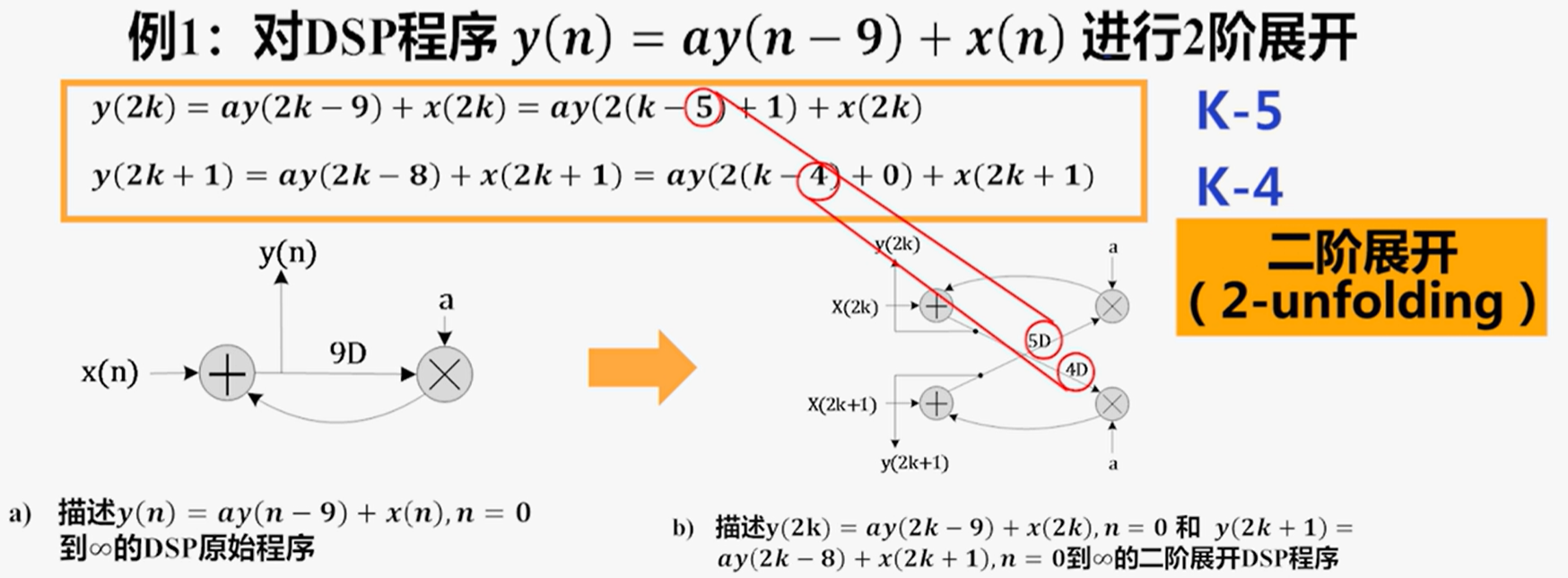
• 展开方法：

  • 符号：

    • $\lfloor x \rfloor$：表示对x向下取整，即取小于或等于x的最大整数
    • $\lceil x \rceil$：表示对x向上取整，即取大于或等于x的最大整数
    • $a \% b$：表示a除以b的余数，其中a和b是整数

  • J阶展开DFG的节点与边：

    • 节点U：有J个具有相同功能的节点$U_i(i=0,1,\cdots,j-1)$
    • 边：有J条相应的边
    • 即：J阶展开后的DFG总是包含了相当于原始DFG的J倍数量的节点和边

  • 构建一个J阶展开DFG：

    • 对原始DFG中的每个节点U，画J个节点$U_0,U1,\cdots,U_{J-1}$

    • 对原始DFG中的每个延时为w的边$U\rightarrow V$，画延时为：
      $$
      W_{new}=\lfloor \frac{(i+w)}{J} \rfloor的J个边U_i\rightarrow V_{(i+w)\%J}(i=0,1,\cdots,J-1)
      $$

• 例：3阶展开

  

---

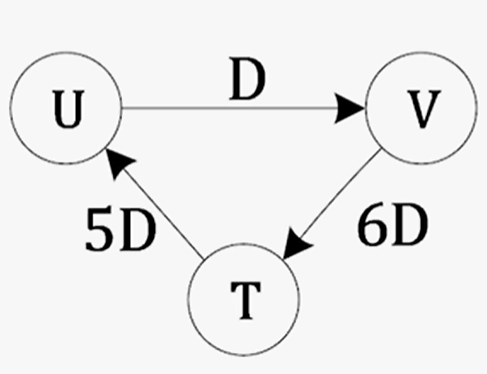
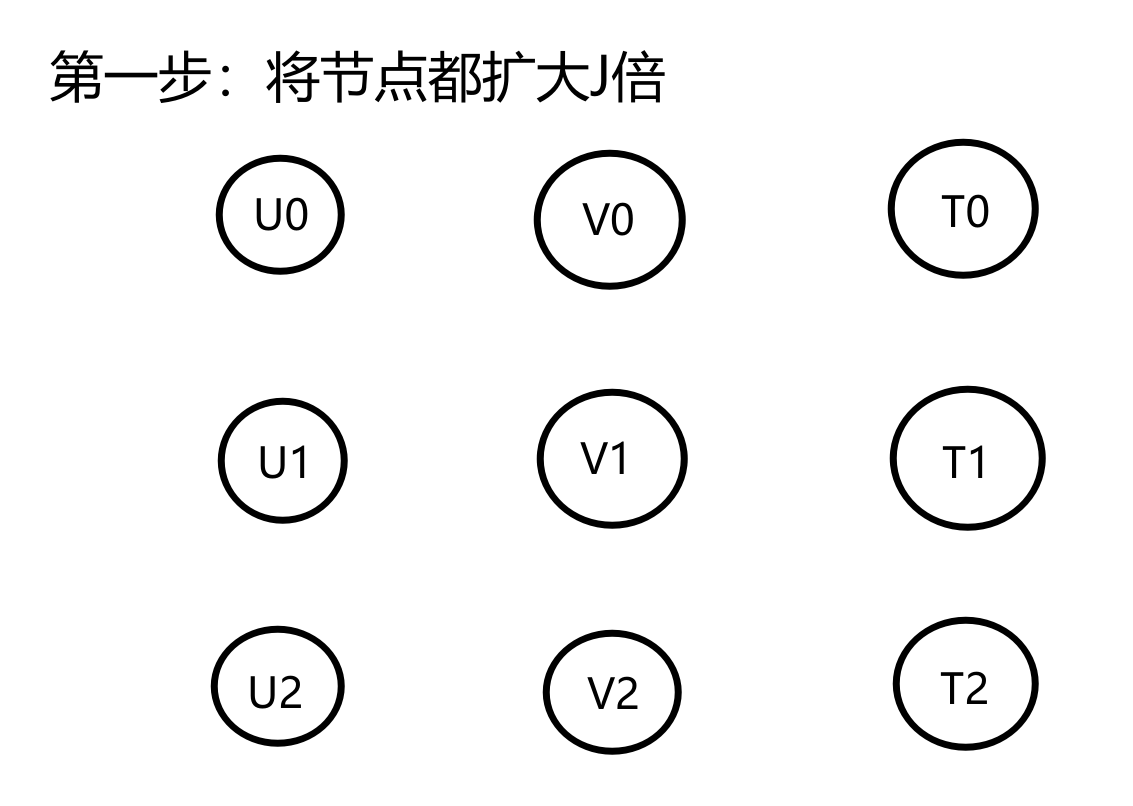
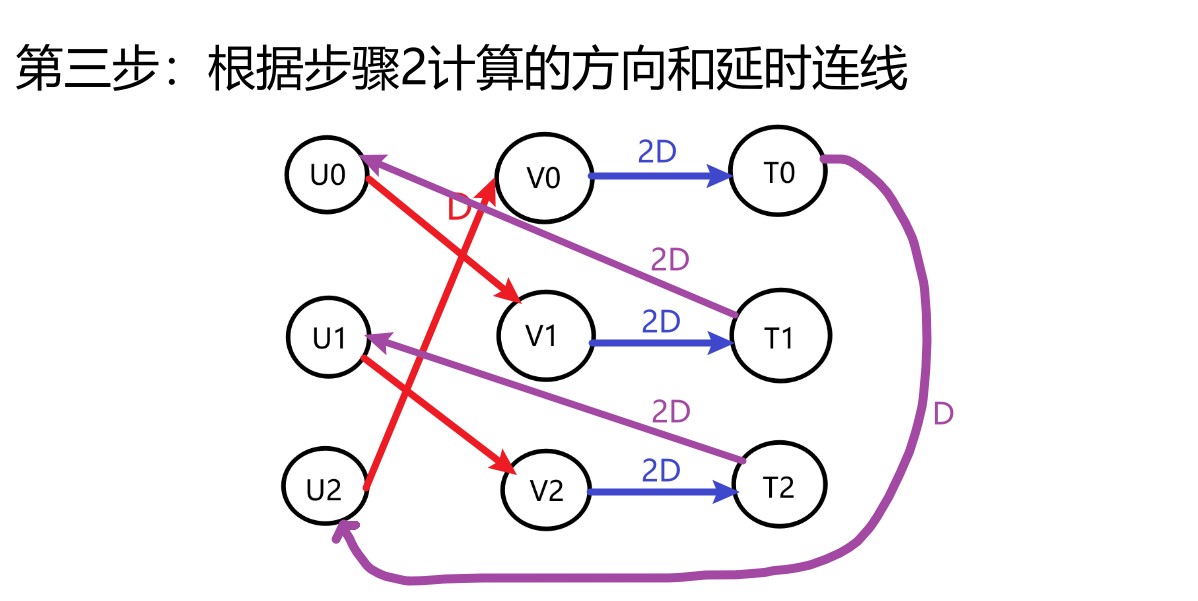
展开的基本性质

• 展开保留原DFG中各边的优先约束

• 展开保持原DFG中个边的延迟数

• 展开对关键路径的影响：

  • 原图G中$w<J$的边在J阶展开中生成$J-w$条无延迟的边和$w$条延迟为1的边（无延迟边的增加意味着关键路径可能增加导致时钟周期增加、频率降低）
  • 原图G中$w\ge J$的边在J阶展开中生成J条延迟$\ge1$的边，不会生成无延迟边，则不会增加关键路径

• 展开环路的影响：

  • 原图G中延时为$w_l$的环路l，在J阶展开中有$gcd(w_l,J)$（gcd为最大公约数）个环路，每个环路包含了$\frac{w_1}{gcd(w_1,J)}$个延迟
  • 展开环路使得迭代边界增加：迭代边界为$T_{\infty}$的原图G中的J阶展开的迭代边界为$JT_{\infty}$

• 例：

  

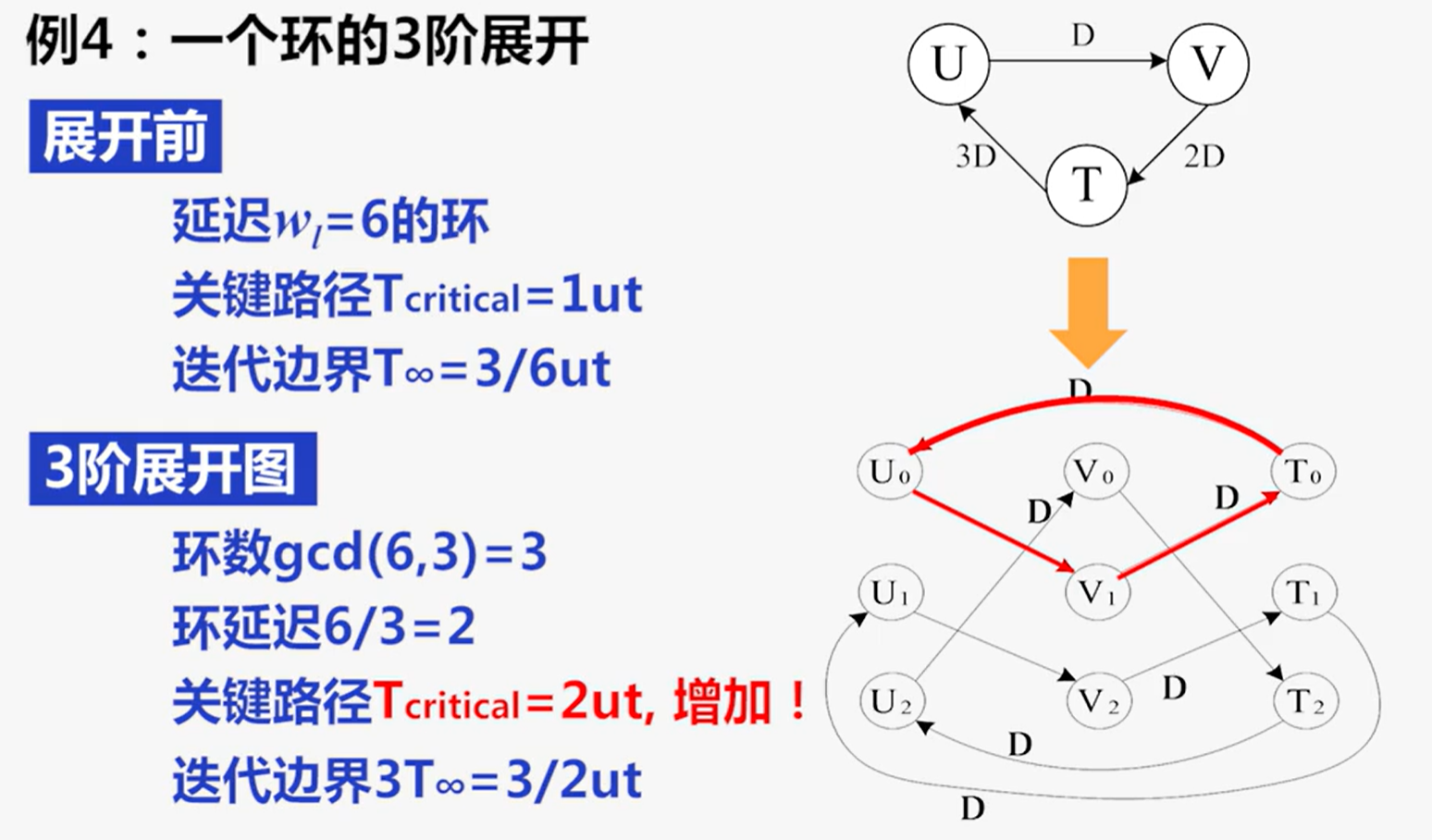
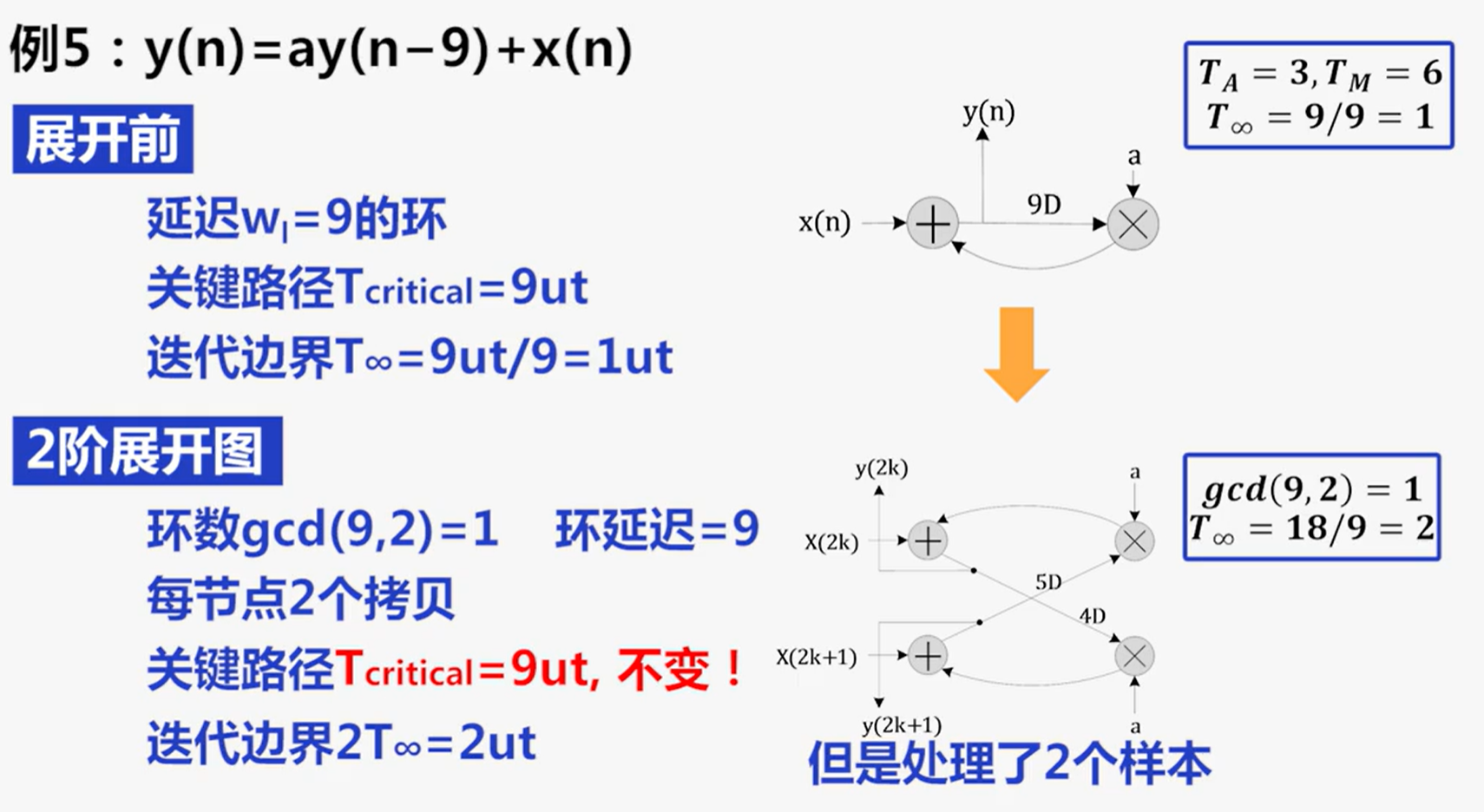
• 提高采样速度，让采样周期逼近原始环路的迭代边界（展开后的关键路径等于迭代边界），实现性能极限

  • 情况1：原始DFG中存在节点的计算时间$T_U>T_{\infty}$

    • 此时：
      $$
      J=\lceil \frac{T_U}{T_\infty}\rceil
      $$

<img src="VLSI%20DSP%E4%B9%8B%E5%B1%95%E5%BC%80/image-20221124172334012.png" alt="image-20221124172334012" style="zoom: 33%;" />

• 情况2：迭代边界$T_{\infty}$不是整数

  • 此时：
    $$
    J=\frac{w_l}{gcd(T_l,w_l)},T_l为环路的执行时间，w_l为环路的延时
    $$
  

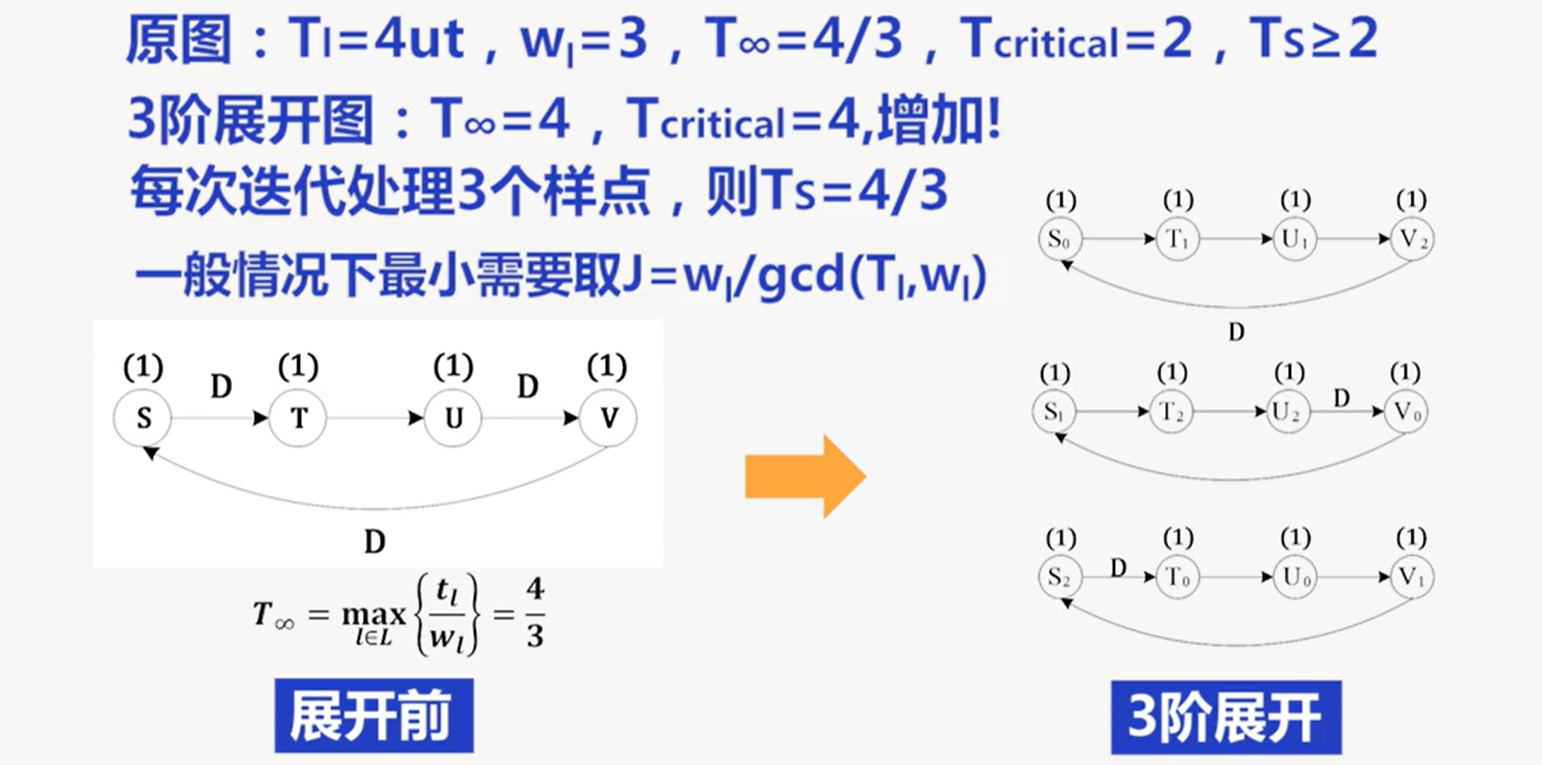
• 情况3：最长的节点计算时间大于迭代边界$T_{\infty}$，同时$T_{\infty}$也不是整数（情况1、2的混合）

  • 此时：
    $$
    J\times T_{\infty}=整数
    $$

    $$
    J\times T_{\infty}\ge T_u
    $$

    通过满足上述不等式求得最小的$J$